depth-first search

depth-first search is an algorithm for traversing graphs.
dfs starts at an arbitrary vertex $\text{[math]}$ and progresses from neighbor to neighbor.

a free vertex is one that hasnt yet been visited

during the traversal, two timestamps are set for each vertex, discovery timestamp and departure timestamp, each timestamp is a number between 1 and $\text{[math]}$ . each such number corresponds to only one timestamp, the timestamps are stored in the following variables:

discovery time: $\text{[math]}$ which is set when $\text{[math]}$ is first visited during the traversal
departure time: $\text{[math]}$ which is set when $\text{[math]}$ is last departured

next to each vertex is its discovery/departure timestamps

a dfs tree gets built during traversal, if we're at a vertex $\text{[math]}$ and we wanna move to vertex $\text{[math]}$ , then:

if $\text{[math]}$ is free, we move to $\text{[math]}$ and the edge $\text{[math]}$ is a tree edge, and is included in the dfs tree
if $\text{[math]}$ isnt free, we dont move to $\text{[math]}$ . in this case, the edge $\text{[math]}$ is called a back edge in the sense that its directed from $\text{[math]}$ to $\text{[math]}$ and $\text{[math]}$ . $\text{[math]}$ isnt included in the dfs forest

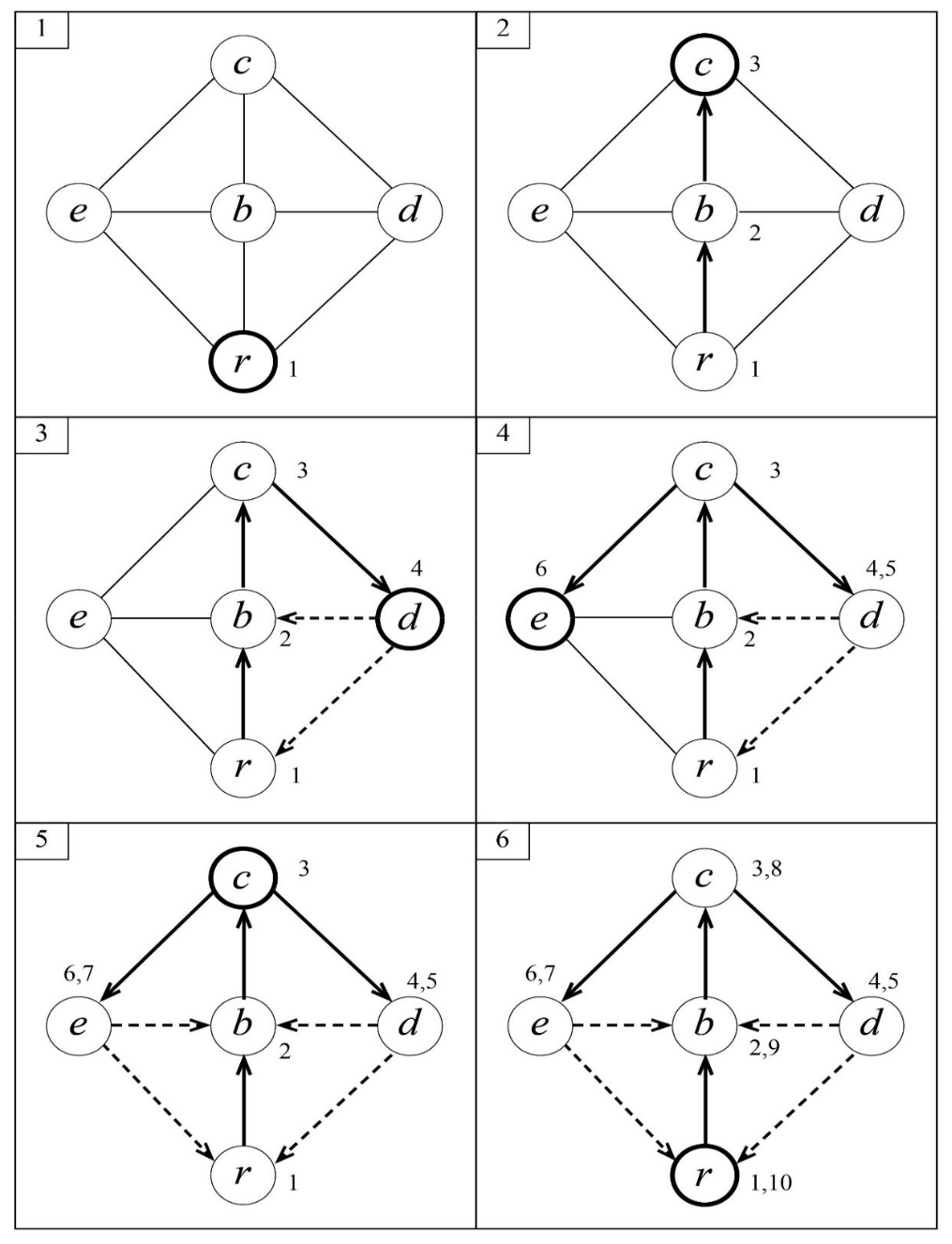
process of a visit

let $\text{[math]}$ be a free vertex, say we're moving from the vertex $\text{[math]}$ to $\text{[math]}$ . before we move to $\text{[math]}$ , $\text{[math]}$ is marked as the vertex previous to $\text{[math]}$ .
when we are at $\text{[math]}$ , at the beginning of the visit, we mark $\text{[math]}$ as a non-free vertex. then we go through each neighbor of $\text{[math]}$ one after another, skipping any neighbors that are marked as non-free.
assume that the neighbor vertex $\text{[math]}$ is free: we mark $\text{[math]}$ as the parent of $\text{[math]}$ , we timestamp the visit in $\text{[math]}$ and start our visit at $\text{[math]}$ . after we're done with $\text{[math]}$ , we retreat to $\text{[math]}$ , and renew our visit at $\text{[math]}$ .
when we've gone through all of $\text{[math]}$ 's neighbors, we're done with our visit at $\text{[math]}$ , we retreat to $\text{[math]}$ .
when we finally retreat to the origin node and there's no more free vertices, the first output tree would be complete. the process is over when there's no vertices left non-visited.
the simplest way to implement this logic is using recursion, which we may see later in the $\text{[math]}$ function.

data structures used

the data structures used in the dfs algorithm are

a global variable $\text{[math]}$ that allows giving timestampts to each $\text{[math]}$ call. the initial value of $\text{[math]}$ is 1.
for every vertex we define 3 variables:
1. $d[v]$: the discovery time of $v$ (value of $time$ at the start of $\textsc{DFS-Visit}$)
2. $f[v]$: the departure time of $v$ (the value of $time$ at the end of $\textsc{DFS-Visit}$)
3. $p[v]$: the preceding node to $v$ in the output tree

pseudocode

$\text{[math]}$ the $\text{[math]}$ function initiates the data structures we need, traversal is done by $\text{[math]}$

further analysis

the total time complexity of the dfs algorithm is $\text{[math]}$

complexity of $\text{[math]}$ is $\text{[math]}$ .
for each $\text{[math]}$ , the function $\text{[math]}$ is executed exactly one time. the complexity of this function is equal to the number of neighbors of $\text{[math]}$ .

let $\text{[math]}$ be a connected undirected graph in which $\text{[math]}$ has been applied. for each vertex $\text{[math]}$ :

the function $\text{[math]}$ is executed once only
$\text{[math]}$

assume $\text{[math]}$ is an edge in an undirected graph $\text{[math]}$ . if $\text{[math]}$ is a tree edge and $\text{[math]}$ , then $\text{[math]}$ is directed from $\text{[math]}$ to $\text{[math]}$

let $\text{[math]}$ and $\text{[math]}$ be neighboring vertices in $\text{[math]}$ (that dfs is being applied to). if $\text{[math]}$ is free at time $\text{[math]}$ then $\text{[math]}$ is a descendant of $\text{[math]}$ in $\text{[math]}$

let $\text{[math]}$ be a graph that dfs is being applied to. the vertex $\text{[math]}$ is a descendant of a vertex $\text{[math]}$ in $\text{[math]}$ iff at time $\text{[math]}$ in graph $\text{[math]}$ there is a path of free nodes from $\text{[math]}$ to $\text{[math]}$

let $\text{[math]}$ be an undirected connected graph that dfs has been applied to starting at the vertex $\text{[math]}$ . then $\text{[math]}$ contains a single rooted tree whose root is $\text{[math]}$

let $\text{[math]}$ be an undirected connected graph. assume that $\text{[math]}$ was applied to $\text{[math]}$ . for each edge $\text{[math]}$ , $\text{[math]}$ is either a tree edge or a back edge.

dfs in a directed graph

its not much different from dfs being applied to an undirected graph except that during traversal we only jump to neighbors that are descendants

an edge $\text{[math]}$ is a forward edge if $\text{[math]}$ is an ancestor of $\text{[math]}$ in $\text{[math]}$ .
if $\text{[math]}$ is a forward edge directed from $\text{[math]}$ to $\text{[math]}$ , then $\text{[math]}$
if $\text{[math]}$ is a cross edge directed from $\text{[math]}$ to $\text{[math]}$ then $\text{[math]}$

topological sorting

$\text{[math]}$

proof of correctness:
assume that $\text{[math]}$ is an edge in $\text{[math]}$ that is directed from $\text{[math]}$ to $\text{[math]}$ . if we were to apply $\text{[math]}$ to $\text{[math]}$ , then $\text{[math]}$ .

time complexity:
same as dfs, $\text{[math]}$